Coresets for Data-efficient Deep Learning

To improve the efficiency and sustainability of learning deep models, we propose CREST, the first scalable framework with rigorous theoretical guarantees to identify the most valuable examples for training non-convex models, particularly deep networks. To guarantee convergence to a stationary point of a non-convex function, CREST models the non-convex loss as a series of quadratic functions and extracts a coreset for each quadratic sub-region. In addition, to ensure faster convergence of stochastic gradient methods such as (mini-batch) SGD, CREST iteratively extracts multiple mini-batch coresets from larger random subsets of training data, to ensure nearly-unbiased gradients with small variances. Finally, to further improve scalability and efficiency, CREST identifies and excludes the examples that are learned from the coreset selection pipeline. Our extensive experiments on several deep networks trained on vision and NLP datasets, including CIFAR-10, CIFAR-100, TinyImageNet, and SNLI, confirm that CREST speeds up training deep networks on very large datasets, by 1.7x to 2.5x with minimum loss in the performance. By analyzing the learning difficulty of the subsets selected by CREST, we show that deep models benefit the most by learning from subsets of increasing difficulty levels.

Read the full article here: paper

Background: Coresets for Efficient Training

When training machine learning models, not all examples are equally important or necessary for achieving good performance. By selecting the most relevant data for training, we can improve the efficiency of the training process.

Recent research has shown that for strongly convex models (linear and ridge regression, and regularized support vector machines), one weighted subset (coreset) is enough to (1) upper bound the gradient error during the entire training, and (2) guarantee convergence for (Incremental) Gradient Descent.

Extracting Coresets for Deep Neural Networks is Challenging!

Because (mini-batch) SGD needs mini-batches with small bias and variance to converge to a stationary point, there are two challenges of extracting coresets for deep models:

Non-convex Loss → High Bias

Loss and gradient change rapidly because of the non-convexity of the loss function → One subset cannot upper bound the gradient during the entire training

Stochastic Gradient → High Variance

One weighted subset selected from the full data has large variance when trained on with mini-batches

Introducing CREST: Coresets for Stochastic Gradient Descent

Modeling the non-convex loss as a piece-wise quadratic

Select one coreset at $w$
Model a quadratic function with Taylor expansion of $\mathcal{L}(w)$
Train on the selected subset as long as the quadratic function has a small approximation error

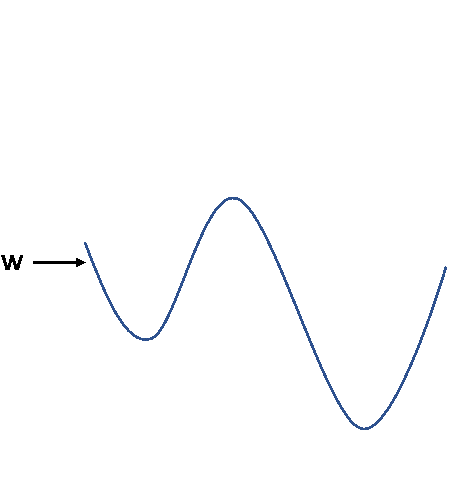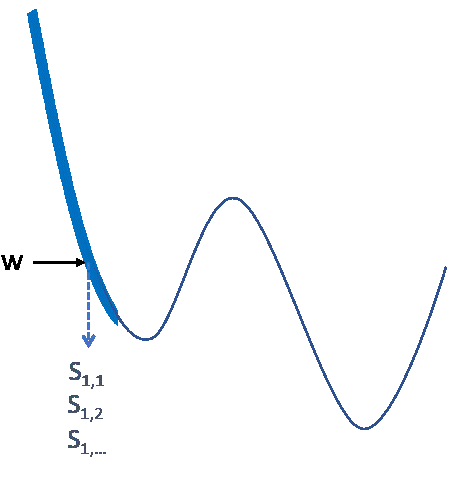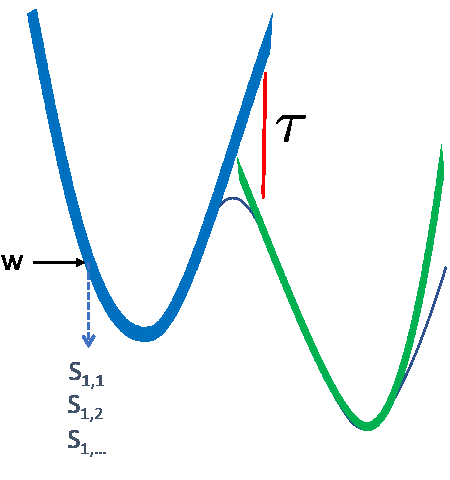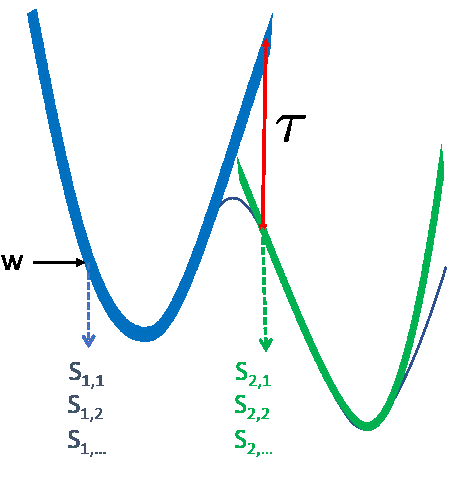
Selecting a single coreset mini-batch coresets from random subsets of all data

Instead of one coreset, we want to find multiple mini-batch coresets from larger random subsets to have smaller variance. Each of the mini-batch coresets is nearly unbiased as long as the quadratic approximation is still valid.

Theoritical Results

Theorem (Informal). Assuming a bounded variance $\sigma^2$ on the stochastic gradient, if the gradient bias of mini-batch coresets is bounded by the gradient norm

the selected coresets have small gradient error at beginning of region
small $\tau$ ensures the error remains small during the region training with stochastic gradient descent on mini-batch coresets found by CREST from random subset of size $r$ converges to a stationary point in the following number of iterations:

$$\mathcal{O}(\frac{L(\mathcal{L}(w_0)-\mathcal{L}^*)}{\nu^2}(1+\frac{\sigma^2}{r\nu^2}))$$

Emprical Results

CREST outperforms state-of-the-art coreset selection baselines

CREST speedups training on image and language data

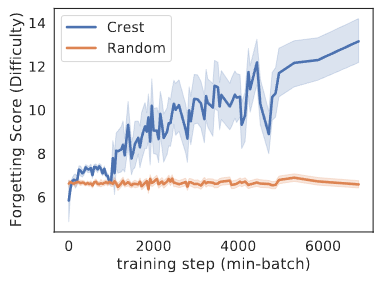
CREST reveals what data is good for deep models

Deep models needs data of increasing difficulty

BibTeX

@inproceedings{yang2023towards,
      title={Towards Sustainable Learning: Coresets for Data-efficient Deep Learning},
      author={Yang, Yu and Kang, Hao and Mirzasoleiman, Baharan},
      booktitle={Proceedings of the 40th International Conference on Machine Learning},
      year={2023}
    }

Code